本文共 4768 字,大约阅读时间需要 15 分钟。
提取阿尔法狗中的灵感
还记得2016年3月9日-3月15日在韩国首尔上演的围棋界终极挑战吗?在总计五轮的人与机器的对决,人类一方的代表——世界围棋冠军李世石很不幸完败于机器一方的代表——美国Google公司旗下DeepMind团队开发的围棋人工智能程序AlphaGo(“阿尔法狗”),这个结果引起了人工智能领域巨大的轰动,也引发了人们对阿尔法狗核心技术的深入研究。
这场终极对决可谓是意义深远,AlphaGo的胜利意味着人们对人工智能的探索已经到达了一个新的阶段。早期传统的棋类软件一般采用暴力穷举法,也就是把棋盘上所有可能局面一一列举出来建立搜索树,并遍历搜索树从中筛选最优势的走法。不过这只能适用于解决效率低,规模小的问题。由于围棋是一种复杂且深奥的游戏,一方面围棋的每一步可能性非常多,另一方面落子选择在某种程度上依靠棋手经验积累,因此在瞬息万变的局面下,计算机很难分辨当下棋局的优势方和弱势方。可见攻克围棋一直被认为是人工智能领域中的一个巨大挑战。
AlphaGo则采用了深度神经网络、监督/强化学习、蒙特卡洛树搜索这三个“利器”的结合完美解决了以上这些问题。下面简单了解下这三个“利器”,看下是哪件“利器”解决了搜索棋局样本空间巨大这个问题。
关于深度神经网络,AlphaGo包含策略网络和估值网络。策略网络主要是用来生成落子策略,它会根据棋盘当前的状态,搜索出最符合人类高手的几种可行的下法位置。但是策略网络只知道这步棋是否跟人类下的一样,并不知道这步棋到底下得好不好,这时候需要估值网络为各个可行的下法评估出一个“胜率”,策略网络结合“胜率”最终确定落子的策略。
关于监督/强化学习,AlphaGo背后是一群杰出的计算机科学家,在初始阶段,科学家利用神经网络算法将大量棋类专家的比赛数据输入给AlphaGo,使它学习人类棋手的下法,形成自己独特的判断方式。之后,在不计其数的自我模拟对弈,以及每一次与人类棋手对弈中,总结并生成自己的“经验”,实现自我提高。
关于蒙特卡洛树搜索,在从根结点开始选择要搜索的分支子结点时,每一次决策都会同时产生多个可能性,AlphaGo对这些可能结果进行仿真运算,根据估值网络反馈的胜率作出最优决策,通过不断的推演使得游戏局势向预测的最优点移动,直到模拟游戏胜利。

对于解决如何在搜索样本空间巨大的情况下搜索出更好的节点,蒙特卡洛树搜索法MCTS(Monte Carlo Tree Search)起到了至关重要的作用。单从字面意思上蒙特卡洛树搜索法可理解为在树搜索方法上融入蒙特卡洛法,将随机模拟的思想应对于大量不确定样本的情况下。通过不断的模拟得到大部分节点的估值,然后下次模拟的时候根据估值有针对地选择值得利用和值得探索的节点继续模拟,在搜索空间巨大并且计算能力有限的情况下,这种启发式搜索能更集中地、更大概率找到一些更好的节点。那么随机模拟的蒙特卡洛算法又是如何实现的呢?
深入了解蒙特卡洛思想
蒙特卡洛(Monte Carlo)法确切地说是一类随机模拟算法的统称,提出者是大名鼎鼎的计算机之父冯·诺伊曼,因为在赌博中体现了许多随机模拟的算法,所以他借用驰名世界的赌城—摩纳哥的蒙特卡洛来命名这种方法。
此处以网络上普遍采用的例子加以扩展来解释下蒙特卡洛法的思想。
假如篮子里有1000个苹果,让你每次闭着眼睛拿1个,挑出最大的。于是你闭着眼睛随机拿了一个,然后再随机拿一个与第一个比,留下大的,再随机拿一个,与前次留下的比较,又可以留下大的……你每拿一次,留下的苹果至少是当前最大的,循环往复这样,拿的次数越多,挑出最大苹果的可能性也就越大,但除非你把1000个苹果都挑一遍,否则你无法肯定最终挑出来的就是最大的一个。
这么看来蒙特卡洛法的理论支撑其实是统计概率理论中的伯努利分布。以抛硬币为例,每次抛硬币只有正面朝上或反面朝上两种可能的结果,由于伯努利分布的特点是每次采样是相互独立的,那么前5次抛硬币对于第6次抛硬币的结果没有任何影响。当抛硬币次数的增加到一定次数时会发现正面和反面出现的概率会无限的接近于50%。
挑苹果也是一样的,每次挑出最大的苹果的概率是1/1000(此处概率仅为说明观点,实际上第一次的概率为1/1000,第二次开始为1/999),由于每次挑选是一个独立的事件,在独立事件中1/1000这个概率是始终保持不变的。当挑苹果次数的增加到一定次数时会发现实际挑出最大的苹果的次数会遵循1/1000这个概率。
也就是说,蒙特卡洛法采样越多,越能找到最佳的解决办法,但只是尽量找最好的,不保证一定是最好的。在这种情况下如果要求必须找出最优解,也就是最大的苹果,那还不如采用暴力穷举法逐个比较所有的苹果的大小来的直接,但是如果用这种方法寻找一个连续区间[-2,2]上某个函数的极值时肯定是行不通的,此时更合理的是用蒙特卡罗法在有限采样内,给出一个近似的最优解。我们通过以下计算函数极值的实验了解下蒙特卡洛法的应用。
实验原理:
极值是“极大值” 和 “极小值”的统称。如果一个函数在某点的一个邻域内处处都有确定的值,当函数在该点的值大于或等于在该点附近任何其他点的函数值,则称函数在该点的值为函数的“极大值”;当函数在该点的值小于或等于在该点附近任何其他点的函数值,则称函数在该点的值为函数的“极小值”。此处在区间[-2,2]上随机生成一个数,求出其对应的y,找出其中最大值可认为是函数在[-2,2]上的极大值。
实验步骤:
(1)设函数y=f(x)=200*sin(x)e-0.05x
(2)随即取点(X),使得-2 \u0026lt;=X\u0026lt;=2,即点在区间[-2,2]内(3)通过公式 f(x)\u0026gt; f(x)max判断当前点的值是否是最大值(4)每次更新最大值和对应的点。(5)运行结果发现极大值185.1204262706596, 极大值点为1.5144491499169481例程如下:
def cal_extremum_mc(n = 1000000): y_max = 0.0 x_min, x_max = -2.0, 2.0 y = lambda x:200*np.sin(x)*np.exp(-0.05*x)#匿名函数 for i in range(0, n+1): x0 = random.uniform(x_min, x_max) if y(x0) \u0026gt; y_max: y_max = y(x0) x_max = x0 return y_max, x_max
以上例子也称为基于蒙特卡洛的投点法,由此得出的值并不是一个精确值,而是一个近似值。当投点的数量越来越大时,这个近似值也越接近真实值。
金融交易策略的参数优化
科学家们花费大量心血研究AlphaGo并不是为了炫耀在围棋领域能够战胜人类,而是想将它的核心技术推广到各种领域帮助人类解决问题。反观金融领域,在金融市场中又何尝不是充满了随机性和不确定性,那么蒙特卡洛法如何应用到金融领域在不确定的市场中寻求近似确定性的方向呢?
在传统的主观型交易中,那些技术面分析的交易者习惯于围绕盘面各种成熟指标的动态来制定交易策略,比如MACD、KDJ、均线指标等等。其实所有的技术指标都是依据股票收盘价、开盘价、最高价、最低价、成交量等原始的交易数据通过某种算法计算而来的。以最常用的移动平均线来说,10日均线即“之前10个交易日”收盘价的加权平均价,所谓的移动就是将新一个交易日的收盘价加入公式中,同时剔除最早一个交易日的收盘价,不断右移计算输出当日对应的SMA值,然后将它们连接起来构成均线。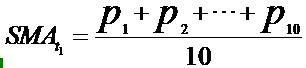
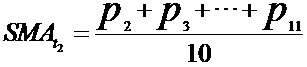
大家是否注意到,在大多数的股票行情软件中默认的均线参数普遍是5日、10日、20日、30日、60日、120日……而非6日、7日、21日之类,在各种介绍炒股秘籍的书中也清一色的告诉读者参照这些默认的参数制定炒股策略。但是这些默认值真的就是最优化的参数值了吗?好像并不见得,那么让我们开始寻找最优化的参数。
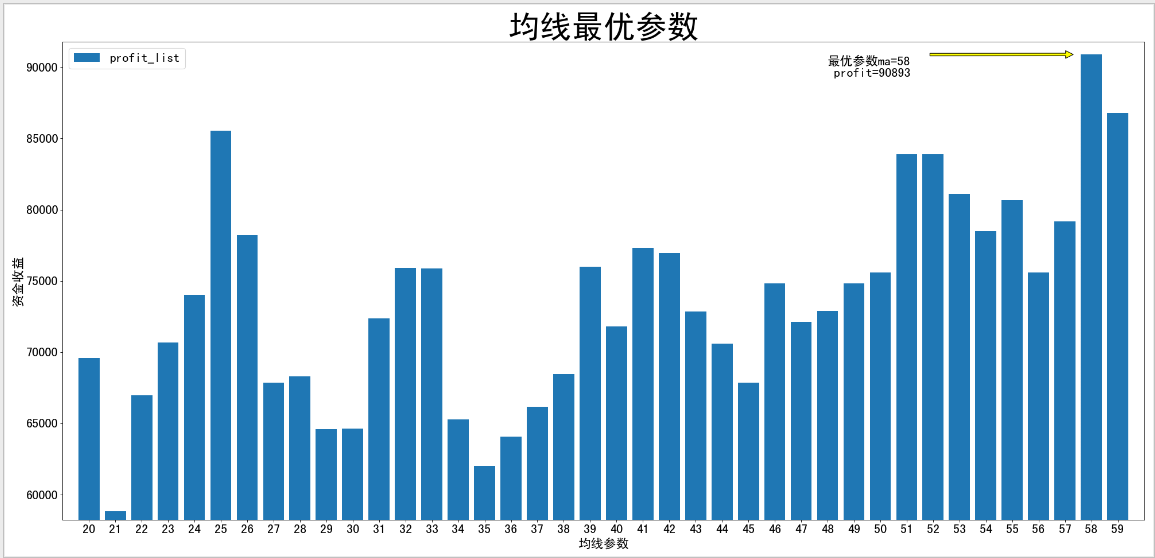
此处我们将一个简单的单均线突破策略应用于浙大网新上进行回测。单均线突破的交易策略为:若昨日收盘价高出过去N日移动平均线则今天开盘即买入股票;若昨日收盘价低于过去N日移动平均线,那么今天开盘卖出股票。我们用暴力穷举法遍历了20至60日均线之间的所有均线参数,发现资金收益最高时所对应的移动平均线的最优参数是58日,而并非通用的60日。
近几年来金融量化交易发展愈来愈火爆,借助计算机的强大性能,运用数据建模、统计学分析、程序设计等工具制定交易策略已经成为金融交易市场的一个大的发展趋势。因此相对于传统的主观型交易,策略参数的最优化过程在量化交易中变得更便捷。那么在制定策略过程中如何选择策略的最优化参数呢?
显然,暴力穷举法只能适应于上述小规模遍历20至60日均线之间的参数,而对于稍复杂一些的策略模型,如双均线突破策略就需要两组参数样本空间两两排列组合。双均线突破策略为:当短期均线穿过长期均线,同时往上时认为上升趋势成立,作为买入信号;当短期均线穿过长期均线,同时往下时认为下跌趋势成立,作为卖出信号。如果短期均线参数样本范围为 [10,50],长期均线参数样本范围为 [50,90],那么需要遍历的参数组合就有1600组,再叠加其他指标的参数种类后样品空间会变得非常巨大。
再从金融市场和量化交易策略模型本身来看,市场在变化,信息在变化,过去并不代表未来,用历史数据作量化策略的回测检验是把过去的经验作为一种参考指南,通过对过去的解读发掘出蕴藏盈利机会的重复性模式。这就像在正式高考前学校都会定期组织模拟考来评估下自己的能力,显然最终的高考题目不会和模拟考一摸一样,但在模拟考发挥的水平正常情况下和高考发挥的水平相差不会太大。 可见我们并不需要一成不变的固定参数值,而是持续不断的更新接近于最优的策略参数值。
因此蒙特卡洛法成为了参数最优化的首选方案。以下例程为分别在短期均线和长期均线的样本空间中随机生成均线参数的方法,而后可将采样的组合参数代入策略中进行回测分析。
例程如下:
def cal_moveavg_mc(n = 500): avg1_min, avg1_max = 10, 50 avg2_min, avg2_max = 50, 90 ma_list = [] for i in range(0, n+1): avg1 = int(random.uniform(avg1_min, avg1_max)) avg2 = int(random.uniform(avg2_min, avg2_max)) ma_list.append([avg1,avg2]) #此处添加回测采样参数 return ma_list
总结
本文简要介绍了AlphaGo的三个“利器”,以及解决搜索棋局样本空间巨大这个问题所采用的蒙特卡洛树搜索法,进一步从中提取蒙特卡洛法应用于量化交易的策略参数优化中。量化交易的本质是管理胜算的概率,而蒙特卡洛法的随机过程同样是以概率的形式求取近似的解,笔者认为在充满不确定性的金融市场中,将蒙特卡洛法应用于量化交易的策略参数最优化过程,能够在参数样本空间巨大的情况下择优选出策略参数,值得在业界进行推广。
作者介绍
元宵大师,Python高级工程师,公众号《元宵大师带你用Python量化交易》作者,致力于推动人工智能在金融量化交易领域中的应用。
转载地址:http://zdbso.baihongyu.com/